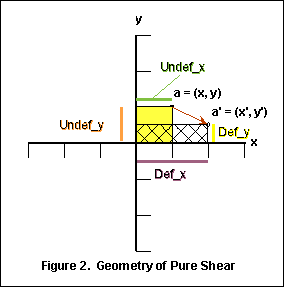
The geometry that we will use in analyzing pure shear is shown in Figure 2.
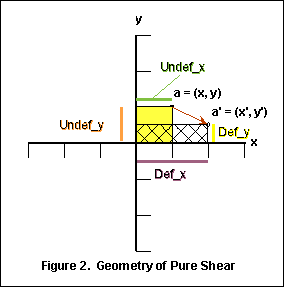
Note that our starting coordinate is labeled a and during pure shear it is translated to a’. Def_x is the perpendicular distance from the y axis to point a’. Undef_x is the perpendicular distance from the y axis to point a. The ratio Def_x/Undef_x is the proportional change in position along the x axis that a has undergone relative to its original position as it was translated during pure shear. An important measurement of strain is stretch, which is defined as Def_x/Undef_x. As shown in the section entitled Measurements of Strain, stretch is also defined as (e + 1), where elongation (i.e., e) = (Def_x – Undef_x)/Undef_x. Thus, the coordinate transformation equation for x’ is
(5) x’ = ((e + 1)*x) + (0*y).
In order to obtain the coordinate transformation equation for y’, we first note that pure shear is a constant volume process. Thus, the area occupied by the yellow square in Figure 2 has to be the same as the area of the cross-hatched region which represents its deformed equivalent. Mathematically, we then write
Area of yellow = Area of cross-hatched region.
The area of the cross-hatched region is Def_x * Def_y, thus we have
Area of yellow/Def_x = Def_y.
But Area of yellow also equals Undef_x * Undef_y, and we can therefore write
(Undef_x * Undef_y)/Def_x = Def_y.
Thus, Undef_x/Def_x = 1/(Def_x/Undef_x) = 1/(e + 1), hence
(1/(e + 1)) * Undef_y = Def_y.
We therefore write the coordinate transformation equation for y’ as
(6) y’ = 0*x + (1/(e+1)) *y.
Equations (5) and (6) also can be written in matrix format as follows:
The 2 X 2 matrix on the right hand side of equation (7),i.e.,
is referred to as the strain or transformation matrix for pure shear.