As noted in previous chapters, during homogeneous strain a circle or sphere are transformed into an ellipse or ellipsoid respectively. Structural geologists refer to the resulting ellipse or ellipsoid as the strain ellipse or strain ellipsoid. During transformation of a sphere into a strain ellipsoid there will be at least three material lines that do not rotate relative to reach other (van der Pluijm and Marshak, 1997). These three material lines remain perpendicular before and after strain and are referred to as the principal strain axes X, Y, and Z. The lengths of X, Y, and Z define the strain magnitude with X > Y > Z. In the special case of plane strain, the length of the Y principal strain axis is the same as the diameter of the original sphere. Hence, for plane strain sections perpendicular to Y adequately describe the final strain state.
Material lines are imaginary lines that extend through material points(van der Pluijm and Marshak, 1997). For example, consider an irregular 2D volumetric element of sandstone. Now connect the centers of some grains by material lines as illustrated in the following sketch.
Let us now conduct a simple experiment where we distort our initial irregular 2D volumetric element of sandstone by plane simple shear and plane pure shear.
Experiments like those that you just observed imply that if we know the original configuration of the constituents of some elementary volume of rock material, then we should be able to measure rotations and changes in the lengths of material lines within that volume of rock that are the result of strain.
Structural geologists measure changes in the lengths of material lines as elongations, stretches, and quadratic elongations while rotations are measured as angular strains. Mathematically, these differing measures of strain can be expressed as follows:
Longitudinal Strain or Elongation
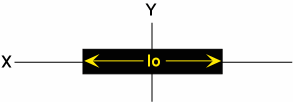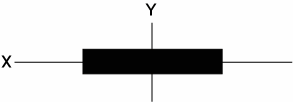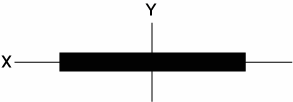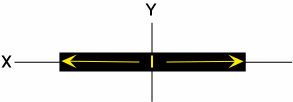
e=(l - lo)/lo where e= elongation or longitudinal strain, l = deformed length, and lo = original length.
Quadratic Elongation
l = (l/lo)2 = (1 + e)2 where e, l, and lo are as defined above.
Stretch
l1/2 = (l/lo)2 = 1 + e, where e, l, and lo are as defined above.
Angular Strain
g = tan(y) where g is angular shear strain and y is angular shear.
